慢接口优化之回溯算法应用

阅读前置条件：了解深度优先搜索回溯算法技巧

背景

每到月初月末的时候，系统都会达到使用高峰。使用人数的增加难免会出现一些平时不能发现的问题，比如在平时响应很快的接口突然变得缓慢，甚至影响到系统的稳定性。这些接口在平时比较难以发现，在没有专业的压测流程的情况下很容易被忽略。今天优化的接口也是这种情况之一，在预发布环境和线上环境都能好好运行，且满足接口响应时间限制，但是到了线上高峰大流量的使用时段，接口就显著变慢。

接口需求

该接口用于计算员工的KPI、相关订单、升星进度信息

由于公司内部一些规定不方便粘贴源码，我将接口抽象到下面的代码中：

数据库建模

CREATE TABLE data_a
(
    id       INT AUTO_INCREMENT PRIMARY KEY,
    order_id varchar(26) not null default ''
    -- 其他相关字段
);
CREATE TABLE data_b
(
    id      INT AUTO_INCREMENT PRIMARY KEY,
    setting varchar(10)
    -- 其他相关字段
);
CREATE TABLE data_c
(
    id            INT AUTO_INCREMENT PRIMARY KEY,
    progress_info varchar(10)
    -- 其他相关字段
);
CREATE TABLE junction
(
    id   INT AUTO_INCREMENT PRIMARY KEY,
    a_id INT comment '订单表',
    b_id INT comment 'KPI规则表',
    c_id INT comment '进度表'
);

即可以简单理解为：将data_a、data_b、data_c表中的数据处理完成后整理到junction表中，并对a、b、c三张表建立一个多对多的关系，供其他系统使用

排查思路

Redis缓存是否被击穿或穿透？
MySQL数据库索引是否合理且正常？
是否有大事务？
代码时间复杂度太高？
本身设计是否合理？

排除流程

通过和DBA方的沟通并结合自己的所学，可以排除数据库层面的（思路1、2）问题。（这里如何确定是数据库问题，可以先走Redis调优和MySQL调优流程）

那么我们现在的重心就落到了排查（是否有大事务？和代码时间复杂度是否太高？）上面

🦀是否有大事务？

大事务：粗略的理解为数据量大，执行时间长的MySQL事务操作。常在批量操作的时候出现

很明显从数据库建模可以看出data_a表中数据量较大，需要重点关注。

分析数据量：

员工在某个时间段（一个月）完成的订单数量大致在200到400左右不等，员工数量（特定的员工才处理）大致在200-300。

极限情况下，需要处理12万左右，为了可靠性，我们将接口吞吐设计到15万。

到此，如果一次性处理完所有逻辑，必定是一个大事务。

处理

小批量多线程处理订单信息（多线程还需要考虑数据丢失怎么处理……）
清理代码中的事务逻辑，拆分大事务，前置查询等操作

（这篇文章讲算法优化，所以简述事务优化）

🦀代码时间复杂度太高？

还记得在MySQL建模部分，我们最终需要将 a、b、c中的操作数据清洗到一张宽表(junction)中供其他系统使用

原有逻辑抽象出来的代码：

public class Polymerization {
    private String a;
    private String b;
    private String c;
    // 省略
}

数据整合逻辑：

实际项目中使用了stream来处理，这里只是将业务代码抽象了

private void demo1() {
    List<String> a = new ArrayList<>();
    List<String> b = new ArrayList<>();
    List<String> c = new ArrayList<>();
    a.add("a1");
    a.add("a2");
    b.add("b1");
    b.add("b2");
    c.add("c1");
    c.add("c2");

    List<Polymerization> res = new ArrayList<>();
    for (String sa : a) {
        for (String sb : b) {
            for (String sc : c) {
                res.add(new Polymerization(sa, sb, sc));
            }
        }
    }
    System.out.println(res);
}

我们可以很清晰的看到目前代码的时间复杂度为：$$O(n^3)$$

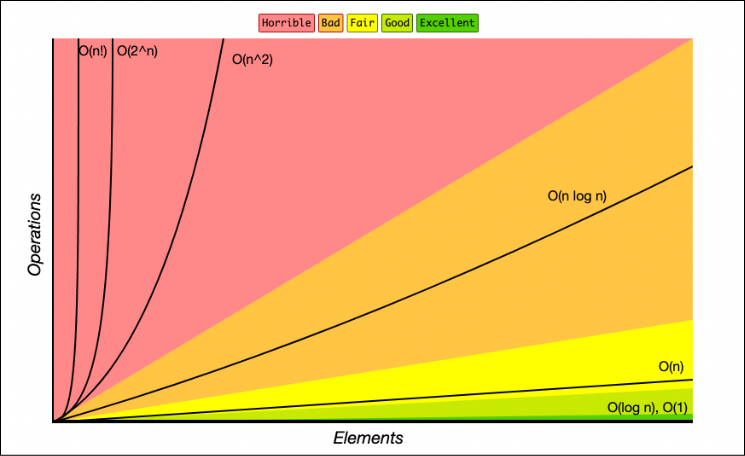
Time Complexity

从上图时间复杂度的函数曲线可以看到 $O(n3)$ 是一条明显陡增的曲线，所以会导致接口请求少的时候没有什么变慢的感觉，但是月底清账需要大数据量处理的时候就会变慢。

至此，我们就可以确定一个最大收益比的点：优化代码的时间复杂度

优化思路

可用算法

由于多层循环导致的时间复杂度变高，那么我们第一个思路就是降低循环次数，用于解决具有多重循环结构问题的方法大致有：

分治处理（Divide and Conquer）
深度优先搜索回溯（Depth-First Search Backtracking）

分治处理（Divide and Conquer）：

思想：将一个大问题划分为若干个子问题，递归地解决子问题，然后将子问题的解合并得到原问题的解。
实现：通常通过递归函数来实现。在每一层递归中，将问题分成两个或多个较小的子问题，然后对每个子问题进行递归调用。最后将子问题的解合并得到原问题的解。
时间复杂度：通常情况下，分治算法的时间复杂度可以用递推关系式来描述，如T(n) = a * T(n/b) + f(n)，其中a表示划分的子问题个数，b表示问题的规模缩小的比例，f(n)表示合并子问题的时间复杂度。时间复杂度可以通过主定理（Master Theorem）进行求解。

深度优先搜索回溯（Depth-First Search Backtracking）：

思想：通过递归地尝试每个可能的解决方案来解决问题。当发现当前尝试的解决方案不能达到目标时，回溯到上一个状态，尝试其他的选择。
实现：通常使用递归函数实现。递归函数尝试每个可能的选择，并在每个选择上进行递归调用，然后回溯到上一个状态，继续尝试其他的选择。

算法选择

❓既然我们找到两种方案可以解决多重循环结构带来的问题，那我们具体选择什么呢？

还记得前面我们需要清理出多对多的关系吧，可以理解为每个属性的解决方案（业务中可能是多个属性使用同一个解决方案），而不是将一个对象的属性划分成小的属性去解决，所以我们选择 深度优先搜索回溯（Depth-First Search Backtracking）

可以简单的理解junction中的数据是关于data_a、data_b、data_c表中数据的组合排列问题

private static void dfs(List<List<String>> data, int indexData, int indexA, int indexB, int indexC, Polymerization current) {
    if (indexData >= data.size()) {
        System.out.println(current);
        return;
    }
    if (indexData == 0) {
        for (int i = indexA; i < a.size(); i++) {
            current.setA(a.get(i));
            dfs(data, indexData + 1, i, indexB, indexC, current);
        }
    } else if (indexData == 1) {
        for (int i = indexB; i < b.size(); i++) {
            current.setB(b.get(i));
            dfs(data, indexData + 1, indexA, i, indexC, current);
        }
    } else {
        for (int i = indexC; i < c.size(); i++) {
            current.setC(c.get(i));
            dfs(data, indexData + 1, indexA, indexB, i, current);
        }
    }
}
private static void demo() {
    a.add("a1");
    a.add("a2");
    b.add("b1");
    b.add("b2");
    c.add("c1");
    c.add("c2");
    List<List<String>> data = new ArrayList<>();
    data.add(a);
    data.add(b);
    data.add(c);

    dfs(data, 0, 0, 0, 0, new Polymerization());
}

indexData：表示处理对象中的哪个一批属性，业务自己扩展

indexA\indexB\indexC：该指针是为了防止重复匹配到已经用到的属性。可以理解为数据选取的开始位置。

输出结果：

Polymerization{a='a1', b='b1', c='c1'}
Polymerization{a='a1', b='b1', c='c2'}
Polymerization{a='a1', b='b2', c='c1'}
Polymerization{a='a1', b='b2', c='c2'}
Polymerization{a='a2', b='b1', c='c1'}
Polymerization{a='a2', b='b1', c='c2'}
Polymerization{a='a2', b='b2', c='c1'}
Polymerization{a='a2', b='b2', c='c2'}

总结：

tree

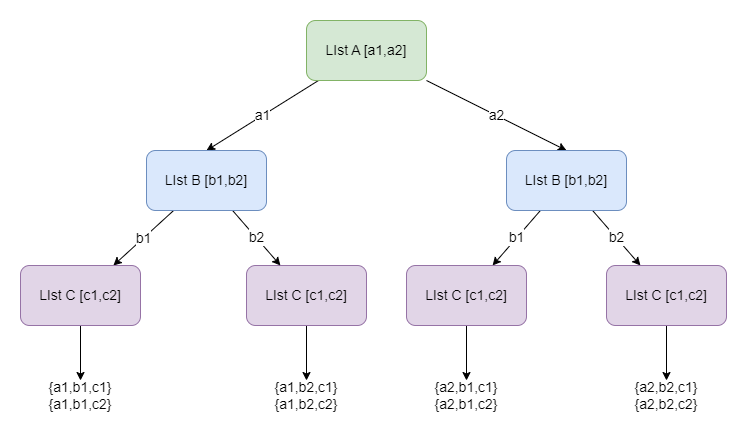
综上所述，其实就是将多个列表的嵌套遍历放到了一颗树中进行，从而降低时间复杂度。

但这种解决方案只能在特定条件下使用，且编码和维护都比较困难，需要对DFS和回溯思想有一定的了解，如果编写代码出错也很容易导致栈溢出

如果通过各方面的努力问题还没有得到解决，那就只有考虑这招了：本身设计是否合理？

目录CONTENT